Нахождение суммы углов является базовой операцией в геометрии, которая применяется при решении различных задач. В зависимости от типа углов и условий задачи, методы вычисления могут отличаться.
Содержание
Основные способы сложения углов
- Арифметическое сложение градусных мер
- Графическое построение суммы углов
- Использование тригонометрических функций
- Применение свойств геометрических фигур
Арифметическое сложение углов
Правила сложения
| Тип углов | Пример вычисления |
| Острые углы | 30° + 45° = 75° |
| Тупые углы | 120° + 100° = 220° |
| Углы больше 360° | 400° + 50° = 450° или 450° - 360° = 90° |
Перевод между единицами измерения
- 1 градус = 60 минут (1° = 60')
- 1 минута = 60 секунд (1' = 60")
- Пример: 15°30' + 20°45' = 35°75' = 36°15'
Графический метод сложения углов
Пошаговая инструкция
- Начертите первый угол, отложив его от базовой линии
- От конечной стороны первого угла отложите второй угол
- Результирующий угол будет между начальной линией и конечной стороной второго угла
- Измерьте полученный угол транспортиром
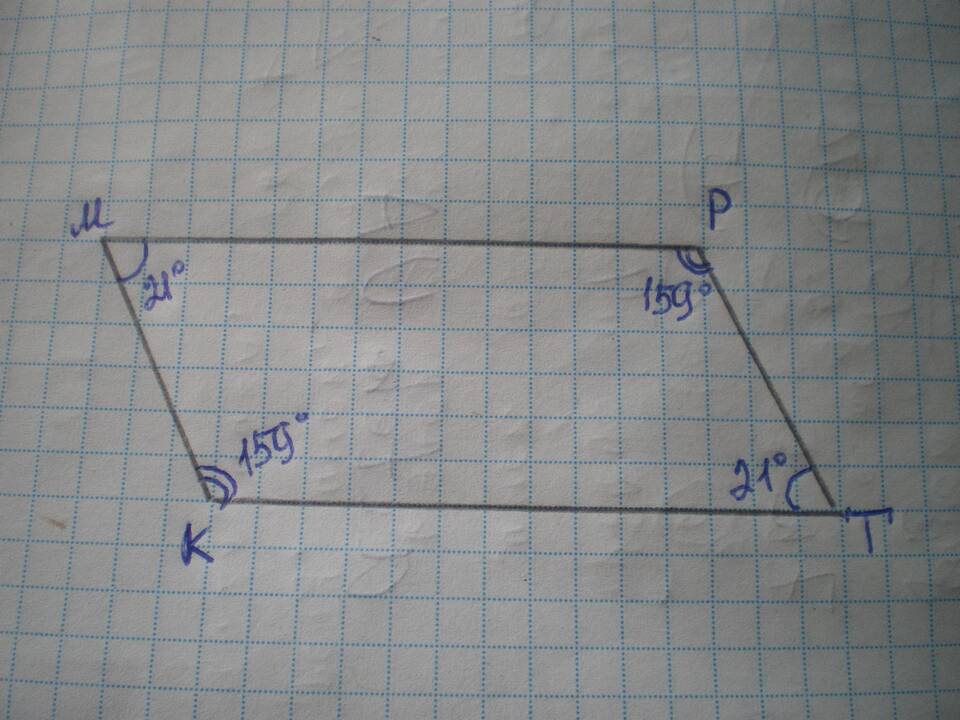
Сложение углов в треугольниках
| Тип треугольника | Сумма углов |
| Плоский | Всегда 180° |
| Прямоугольный | Два острых угла в сумме дают 90° |
| Равносторонний | Все углы по 60°, сумма 180° |
Пример вычисления
- Дано: треугольник с углами 45° и 60°
- Найти третий угол: 180° - (45° + 60°) = 75°
- Сумма двух углов: 45° + 60° = 105°
Тригонометрический подход
Формулы сложения углов
- sin(α + β) = sinα cosβ + cosα sinβ
- cos(α + β) = cosα cosβ - sinα sinβ
- tg(α + β) = (tgα + tgβ) / (1 - tgα tgβ)
Важные замечания
- При сложении углов в разных единицах измерения необходимо привести их к одной системе
- Результат сложения может превышать 360° - в этом случае следует вычесть полный оборот
- В сферической геометрии сумма углов треугольника не равна 180°
- Для точных расчетов рекомендуется использовать калькулятор
Нахождение суммы углов - фундаментальная операция, которая находит применение в различных разделах математики, физики и инженерии. Понимание основных принципов сложения углов позволяет решать широкий круг геометрических задач.