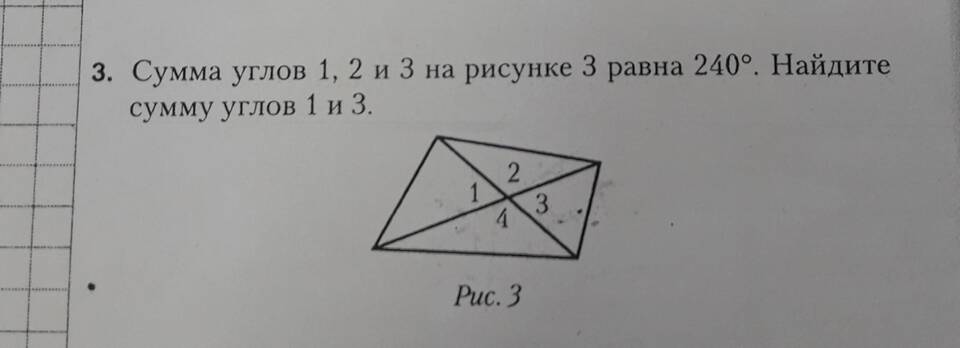
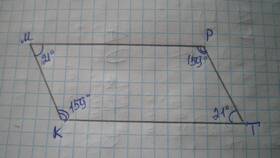
В геометрии существует несколько подходов к определению суммы углов в различных фигурах. Рассмотрим основные случаи, когда требуется найти сумму углов.
Содержание
В геометрии существует несколько подходов к определению суммы углов в различных фигурах. Рассмотрим основные случаи, когда требуется найти сумму углов.
Сумма углов в треугольнике
Для любого треугольника сумма внутренних углов всегда постоянна:
- Сумма углов треугольника равна 180°
- Это свойство верно для всех типов треугольников
- Доказательство основано на аксиоме параллельных прямых
Сумма углов в многоугольнике
Для произвольного n-угольника сумма углов вычисляется по формуле:
| Тип многоугольника | Формула суммы углов |
| Треугольник (3-угольник) | (3-2)×180° = 180° |
| Четырехугольник | (4-2)×180° = 360° |
| Пятиугольник | (5-2)×180° = 540° |
| n-угольник | (n-2)×180° |
Примеры решения задач
- Для треугольника ABC:
∠A + ∠B + ∠C = 180°
- Для четырехугольника ABCD:
∠A + ∠B + ∠C + ∠D = 360°
- Для пятиугольника:
Сумма углов = (5-2)×180° = 540°
Особые случаи
- В прямоугольном треугольнике сумма острых углов равна 90°
- В равностороннем треугольнике все углы по 60°
- В параллелограмме сумма соседних углов равна 180°
Для точного определения суммы углов 1 необходимо уточнить, о какой именно геометрической фигуре идет речь. Приведенные формулы и свойства помогут вычислить искомую величину в каждом конкретном случае.
